量子色动力学（QCD）是描述核子强相互作用的基础理论，其高圈解析计算是具有挑战性的理论难题。而另一方面，超对称场论的研究在近些年取得了很大的进展，比如最大超对称规范场论（N=4 SYM），由于其具有更高的对称性，因此更容易实现高圈计算。 那么，超对称场论的有效计算方法，如在壳幺正性方法，能否有效应用于QCD的高圈计算？超对称场论和QCD是否存在某种直接的联系？近日,中科院理论物理研究所的杨刚副研究员和靳庆军博士在该研究方向上取得重要研究进展, 他们在基于QCD的黑格斯有效场论中，首次得到了包含高维算符的黑格斯粒子和三胶子两圈解析振幅，并且发现这一结果和N=4 SYM的相关结果有直接对应关系，说明QCD两圈振幅存在有待进一步理解的解析结构。相关研究结果已发表于《物理评论快报》（PRL 121 (2018) 101603）。 

　　场论计算的结果一般由超越函数来表达,超越函数可以根据超越度来分类。比如，有理数或有理函数的超越度为0，圆周率π或者对数函数的超越度为1，而更一般的黎曼zeta数ζ_n或者多重对数函数Li_n的超越度为n。粗略地说，超越度表征了函数的复杂程度。已故俄国著名学者Lipatov和合作者最早发现，N=4 SYM的算符反常量纲可以通过QCD相应结果中的最大超越度部分来得到（见Kotikov, Lipatov, Onishchenko, and Velizhanin, PLB 595(2004)521）。这一对应关系被称为“最大超越性原则”，也就是QCD理论中“最复杂”的最大超越度部分和N=4 SYM的结果等价。这一对应原则目前也只是猜想，没有一般的证明。除了反常量纲，这一对应关系对振幅这类更复杂的物理量是否也适用？反常量纲是不依赖于动力学变量的常数，而振幅是依赖于动量的函数，结构要复杂得多。之前仅有的振幅例子是：在黑格斯有效场论的领头阶，黑格斯三胶子振幅和N=4 SYM中相应形状因子的最大超越度部分是相等的（见Brandhuber, Travaglini, and Yang, JHEP 05(2012)082）。这一例子究竟是一个巧合还是更普遍存在？这需要新的例证来验证。 

　　杨刚和靳庆军的研究考虑了黑格斯有效理论中更高维算符的贡献，得到了非常简洁的两圈解析结果，发现最大超越度对应关系仍然成立。不仅如此，这一研究还进一步发现，对超越度更低的部分，QCD和N=4 SYM也存在对应，即包含有理函数系数的超越度更低的部分在两种理论中也是相等的。这些对应关系表明QCD结果可能存在隐藏的解析结构，有待进一步的理解。这一研究所得到的振幅结果也和大型强子对撞机实验有直接联系，给出了黑格斯有效理论中包含高维算符的S矩阵元解析结果，可以帮助提高理论预言的精度。 

　　针对复杂的QCD两圈计算，这一工作也发展了新的计算思路，特别是将在壳幺正性方法和分部积分（integration by part，简称为IBP）约化方法结合起来。幺正性方法是通过研究振幅的奇点（极点或割线）来构造完整的函数。在超对称理论中，这一方法可以在四维中有效地计算圈图；但在QCD中因为所谓有理项的存在，需要在一般的D维中来计算，这使得计算变得很复杂。此外，黑格斯振幅中有非平面拓扑图的贡献，这也使得被积函数的构造比平面振幅要困难得多。IBP约化，作为圈图积分计算的一个重要技术，它可以把积分约化成一组更简单的积分基底，且这一约化不受维数选取的制约。在采用幺正性方法的同时进行IBP约化，这不仅解决了通常D维幺正性方法的困难，也避免了构造被积函数这一复杂中间过程，此外还提高了IBP约化的效率。这一方法在进一步研究中也可以有效地应用于更高阶算符的计算。 

　　该研究得到了中科院前沿重点研究项目、中科院理论物理前沿重点实验室以及国家自然科学基金委理论物理专款“彭桓武理论物理创新研究中心”的支持。 

　　论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.101603 

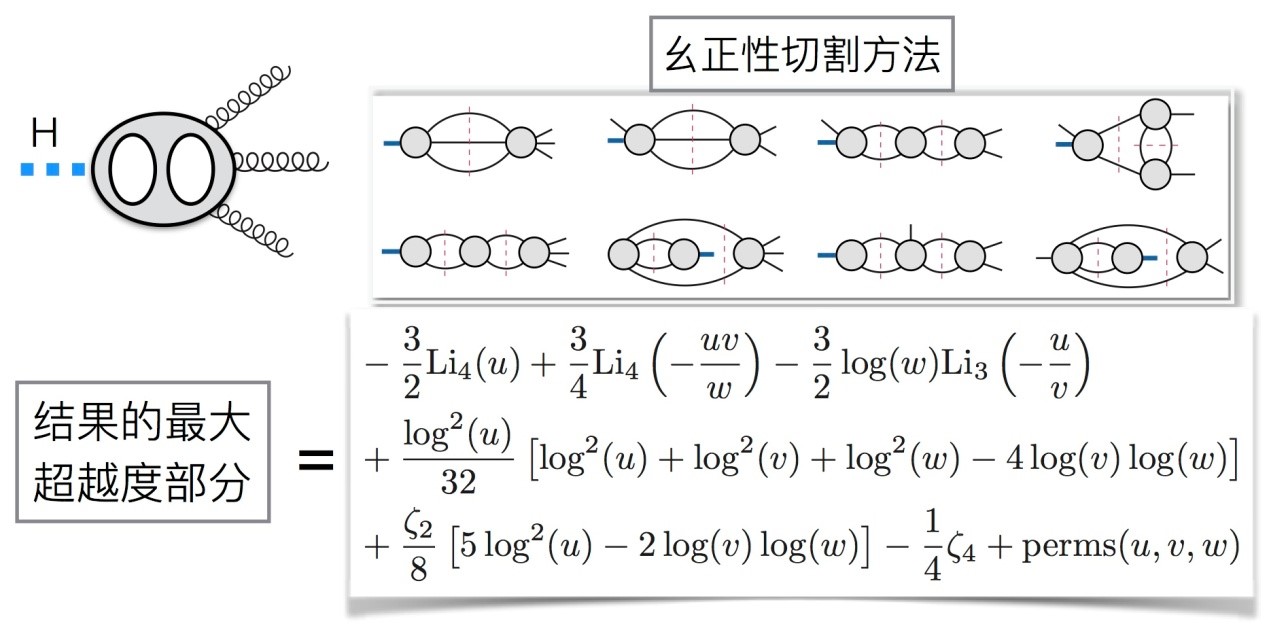
　　附图：黑格斯三胶子两圈振幅的幺正性计算和最大超越度结果