如何计算非平面贡献是场论研究中的一个长期难题。其中，尖点反常量纲（cusp anomalous dimension）作为表征红外发散的基本物理量，其非平面修正计算是十多年来的一个挑战。中国科学院理论物理研究所杨刚和合作者的研究填补了这方面的空白，首次在最大超对称杨-米尔斯理论中计算了尖点反常量纲的四圈（也是领头阶的）非平面贡献，这也是一般四维规范场论中第一次实现的相关计算。该结果首次在微扰水平明确否定了卡塞米尔标度猜想，对于理解场论的红外发散性质具有重要意义。相关研究近日发表于《物理评论快报》（Phys.Rev.Lett. 119 (2017) 201601）。 

　　    场论研究中的一个重要近似方法是取大N极限，对应于将规范群SU(N)的N取无穷大。在该极限下，只有平面拓扑的费曼图有贡献，所以大N极限也称为平面极限。平面极限往往带来很大简化，特别是借助于规范/引力对偶以及可积性，一些重要物理量甚至可以被严格求解。其中，最大超对称杨-米尔斯理论中的尖点反常量纲在大N极限下可以得到非微扰严格解，是近年来超对称场论、可积性和规范/引力对偶研究中最具代表性的重要成果之一（见Beisert, Eden and Stadaucher, J.Stat.Mech. 0701 (2007) P01021）。 

　　    另一方面，作为现实理论的量子色动力学（QCD）的规范群是SU(3)，这时N=3，远偏离于大N极限，非平面贡献不可忽略。规范场中尖点反常量纲的非平面修正从四圈才开始，由于针对平面图的有效方法（比如可积性方法、Mellin-Barnes积分方法等）不再适用，而直接计算非平面四圈费曼积分又极其困难，长期以来其领头阶的结果都是一个空白。也因为如此，关于它的非平面修正存在很多争议，有的学者基于有效场论，预言非平面微扰修正在所有圈都为零（见Becher and Neubert, JHEP 0906 (2009) 081）。这一预言称为卡塞米尔标度猜想，其正确与否，对于理解规范理论的一般红外发散结构非常重要。 

　　杨刚和德国汉堡大学Rutger Boels，锡根大学Tobias Huber合作，突破传统的思路，研究并发展了有效的方法将复杂结果简化为一类特殊费曼积分——这类积分的结果可以由具有同一超越度的超越数来展开。在此基础上的进一步关键发现是，这类同一超越度积分在计算上有极大的简化（其中导致简单性的机理还有待进一步研究），最终得以完成这一极具挑战性的计算。尽管这一研究是针对最大超多称场论，但基于最大超越性原理，该结果也预期给出QCD四圈非平面结果中"最复杂的"的最大超越性部分。这一结果首次在微扰水平明确否定了规范场论（包括QCD）的卡塞米尔标度猜想。此外，这一研究中所发展出来的新方法和新思路也有希望应用于更一般的理论。    

　　该研究工作得到中科院前沿科学重点研究项目的支持。 

　　文章链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.119.201601 

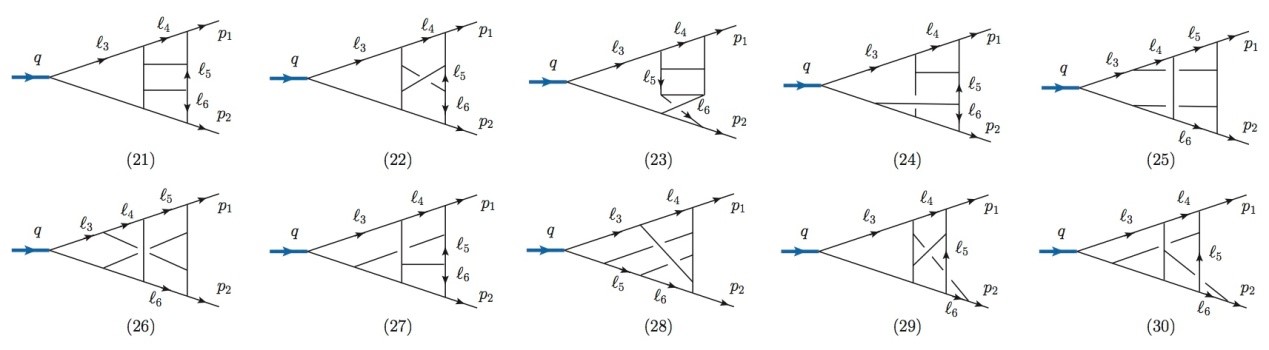
  图：最终贡献于非平面结果的10个四圈费曼积分拓扑