理论物理所在统计物理与复杂系统的研究中取得重要进展
还原能力(Resilience)是很多实际系统最为重要的属性之一,它可很好的刻画物理、生物、生态以及环境系统的鲁棒性和稳定性。在网络系统的研究中,社团(community)结构的探测和描述非常关键。然而,到目前为止,人们对于社团如何影响系统的还原能力和稳定性并不清楚。最近,中国科学院理论物理研究所陈晓松研究员及合作者基于统计物理相变理论攻克了这一难题,该成果已在线发表在世界知名期刊美国科学院院刊(PNAS)上(http://www.pnas.org/content/early/2018/06/19/1801588115?collection=)。
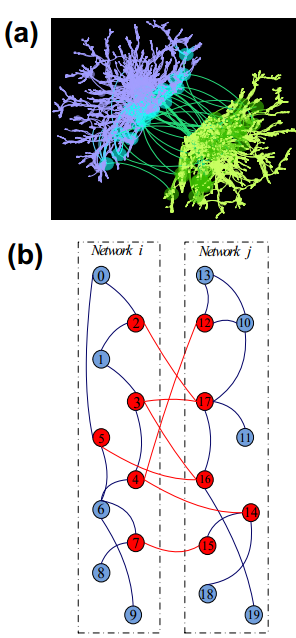
近二十年来网络(network)已兴起为描述复杂系统的一种重要工具。描述实际系统的网络一般具有社团结构,通过攻击网络节点可研究系统的还原能力,发现连接社团的边(interlinks)及相应的节点(interconnected nodes)能显著增加系统的鲁棒性,使得在单一社团网络中能够发生的连续相变消失,消除了连续相变响应函数的发散,系统变得稳定。他们的研究发现,网络系统的社团间连边(interlinks)与铁磁-顺磁自旋系统的外场(external field)作用相似,外场使系统离开其临界点。在临界点附近,社团大小与节点数的关系由临界指数β描述,与社团间连边数的关系由临界指数δ来刻画,其随社团间连边数的变化相当于磁系统的磁化率,由临界指数γ表征。通过理论解析以及数值计算,发现这些临界指数满足Widom’s 等式: δ - 1 = γ/β。
同时,他们将这一理论框架应用到了具有不同社团结构的模型和社会实际网络中(科学家合作网络),发现理论可以完美的预测以及描述实际系统的标度规律和还原能力。这些研究结果不仅能够加深我们对于复杂系统还原能力的理解,更能进一步启发人们对有外场热力学系统的相变研究。
此工作由以色列巴依兰大学樊京芳博士等作为共同一作,巴依兰大学Shlomo Havlin教授,波士顿大学H. Eugene Stanley教授以及中国科学院理论物理研究所陈晓松研究员等参与共同完成。陈晓松研究员的研究小组多年来一直从事统计物理及相关课题的研究,特别是复杂系统的相变与临界现象。樊京芳曾就读于中国科学院理论物理研究所,在陈晓松研究员指导下进行复杂系统的相变与临界现象研究,于2014年获得博士学位。此次发表的工作是相变与临界现象理论与社会复杂系统交叉的研究成果。
此项工作得到中国科学院前沿科学重点研究计划(QYZDJ-SSW-SYS019) 资助。
图:(a)实际网络的community结构,(b)模型示意图。