标准统计物理的建立离不开系综或系统与热库等外界随机源的耦合。能否不引入具虚拟本质的系综概念，对按确定动力学规律演化的“单个”系统直接建立统计物理？这是人们一直在孜孜探索的一个基本物理学问题。早在1929年，冯·诺伊曼就探讨了在量子力学框架下实现对单个系统建立统计物理描述的可能性。自上世纪90年代以来，这方面研究取得了重要进展。特别是M. Srednicki对刚球系统证明，如果量子混沌的Berry猜想成立，那么该系统的单个本征波函数就足以给出费米-狄拉克、玻色-爱因斯坦等热平衡分布。这不仅带来了关于统计物理基础的全新观点，例如复杂系统的单个本征态可等效于一个平衡热库，还建立了统计物理基础和其它以研究波函数涨落为基本内容的学科，尤其是量子混沌和介观物理的紧密联系。 

　　但是，目前绝大部分工作局限在对平衡统计物理基础及趋向热平衡过程（俗称“热化”）的研究。近年来，中科院理论物理研究所田矗舜研究员的课题组致力于探讨微观运动的基本特性之一—波动性—在非平衡统计物理基础中的作用并在近期取得进展。他们揭示了由于微观运动的波动性，非平衡定态和测度集中及一类新介观涨落之间存在深刻联系；相关论文发表于Phys. Rev. Lett. 121, 140603 (2018)。 

　　测度集中是高维几何普遍存在的一个基本现象，由数学家V. Milman在上世纪70年代研究巴拿赫空间的渐进几何时发现；近半个世纪以来，测度集中不仅得到了深刻发展，而且在诸多领域得到了广泛应用。田矗舜研究员的课题组以介观光学的最新发展为背景，把复杂经典和量子波动系统的透射本征通道理论和测度集中理论相结合，研究了具有一般入射波形的单色波在单个无序介质的传播行为。他们以隐藏在该系统的两个高维几何体，即由入射波按本征通道展开所构成的高维球面S^2N-1和由无序介质构形所组成的高维欧基里德空间R^M为出发点，通过把可观测量看成定义在这两个几何体上的函数并论证其Lipschitz连续性，使测度集中理论的应用水到渠成。应用测度集中理论，他们证明了关于波能量密度分布的两个集中不等式，进而严格给出了许多新物理结果。特别地，他们发现改变入射波形产生的介观涨落和传统的改变无序构形产生的介观涨落具有完全不同的普适性，并得到了非传统介观涨落被压制的判据。当这个判据被满足时，不需要热库和系综，非平衡扩散定态就可从几乎所有散射态中自动呈展出来，而可观测量在散射态下的期望值恒等于其本征通道系综（热平衡系综的推广）平均。他们还利用计算机仿真实验完全证实了这些理论预言。这个工作为研究非平衡统计物理基础如不可逆性等提供了全新视角，同时也表明改变入射波形可以诱导丰富的介观涨落现象，对于介观物理特别是介观光学有潜在的应用价值。 

　　此工作得到了国家自然科学基金委重点项目“小量子系统的动力学研究”、中科院理论物理前沿重点实验室和国家自然科学基金委理论物理专款“彭桓武理论物理创新研究中心”的支持。 

　　论文链接：https://link.aps.org/doi/10.1103/PhysRevLett.121.140603 

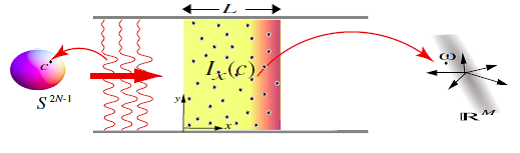
　　附图：隐藏在复杂波动系统中的两个高维几何体