近年来，自旋玻璃研究中发展的复本对称破缺范式在描述阻塞转变问题上取得了突破性进展，某些结构玻璃中被证明存在从简单到具有分形结构的自由能景观的复本对称破缺相变。该转变又被称为Gardner相变，阻塞态被归结为全阶复本对称破缺的Gardner玻璃相的高压/低温极限态。诺贝尔物理学奖获得者Giorgio Parisi等人在无限维极限下，得到了硬球玻璃相的热力学精确解，从而定量解释了阻塞转变的临界性[1]。

然而现实中的无序态大多是在非平衡条件下形成的，对比Gardner物理的普遍性即使在简化的平均场自旋玻璃中仍是尚未解决的问题。此外，在一个系统中取得的非平衡复本破缺问题上的突破有助于推动其他相关复杂系统的研究，动力学复本对称破缺研究因此具有广泛的兴趣和深刻的意义。在最近发表于《美国科学院院刊》（Proc. Natl. Acad. Sci. U.S.A. 120, e2218218120 (2023)）的一项研究工作中，廖沁怡博士和合作者通过模拟简单的硬碟玻璃模型研究该问题。他们分析了反常动力学并定义了动力学转变。另一方面，他们根据自由能景观的复杂性首次给出了完整的玻璃相图。该研究的结果缩小了非平衡条件下的实验和热力学理论研究之间的距离，为构建普适的动力学玻璃理论铺设了道路。

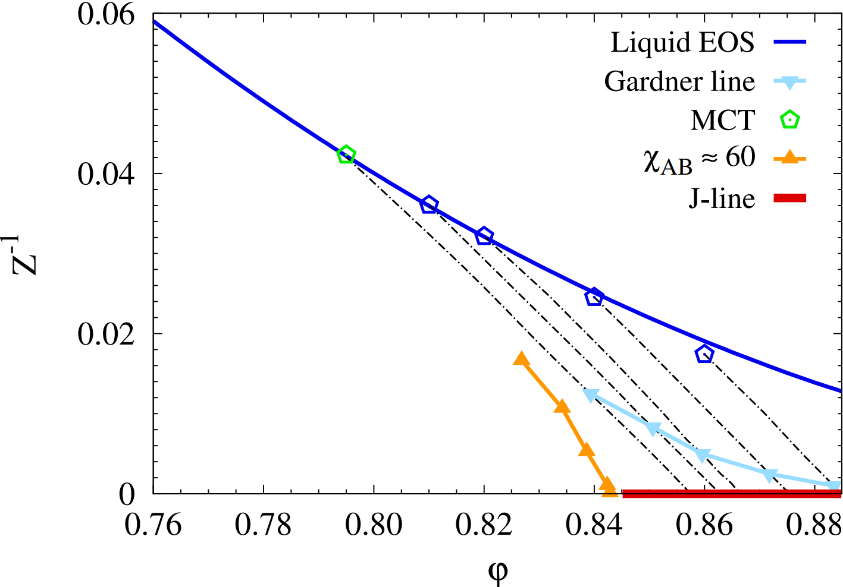
玻璃相图：自上而下，在增大压强趋于阻塞态（红线）的过程中，系统总是先经历Gardner转变（橘线与浅蓝线）。临界阻塞因此受Gardner物理控制。