铜基高温超导t-t'-J模型的有限温度掺杂相图、超导电性及赝能隙--中国科学院理论物理研究所

铜基高温超导t-t'-J模型的有限温度掺杂相图、超导电性及赝能隙

文章来源: 发布时间: 2024-12-23 【字体:大中小】

以Hubbard、 $t\mathrm{-}J$ 模型为代表的强关联电子系统被认为是理解高温超导配对机理的关键。最近，理论物理所/国科大苏刚研究员、李伟研究员与合作者利用有限温度张量网络态方法开展精确多体计算，首次得到了宽度6圆柱面上的 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型温度-掺杂相图，揭示了超导穹顶区域、赝能隙等性质，为深入理解铜氧化物高温超导体的性质提供了重要依据。该工作于2024年12月19日发表在Physical Review Letters，并被选为PRL编辑推荐论文。

自1986年铜氧化物高温超导电性被发现以来，其中的d波超导态、赝能隙、奇异金属态等新奇量子物态一直吸引着人们的广泛关注。高温超导配对机理也被列入Science发布的全世界最前沿的125个科学问题。长期以来，人们认为二维Hubbard模型以及其低能有效理论—— $t\mathrm{-}J$ 模型有可能可以描述电子在铜氧面上的关联物理。然而，Hubbard和 $t\mathrm{-}J$ 模型的求解极为困难，其能否准确描述铜氧化物高温超导是一个长期的公开问题。近年来，人们对该模型的基态研究取得了重要进展，发现尽管只包含最近邻跳迁的Hubbard模型在掺杂下不超导，但通过引入次近邻跳迁 $t^{\prime}/t>0$ ，在宽度6-8的圆柱面上可以得到稳定的d波超导基态；另一方面，在 $t^{\prime}/t<0$ 的情况下是否存在超导态尚存争议[1-4]。上述关于 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型的工作主要针对零温情形，对其有限温度相图的研究相对缺乏。一些亟待解答的重要问题包括， $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型的超导特征温度如何估计，超导相上方是否存在赝能隙等奇异的正常相，与铜氧化物掺杂-温度相图的联系如何等。

利用自主发展的先进有限温度张量网络方法——切空间张量重正化群方法[5]，研究团队在最大宽度6的圆柱面上，对 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型开展了精确的多体计算研究，得到包括 $t^{\prime}/t>0$ 和 $t^{\prime}/t<0$ 情形的温度掺杂相图。结果表明，在 $t^{\prime}/t>0$ 一侧存在穹顶状均匀d-波超导区域，且最佳掺杂的超导特征温度为 $T_c^*/J{\sim}O(0.1)$ ，说明 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型中可以通过自旋交换产生相当高的超导温度。而在 $t^{\prime}/t<0$ 一侧，发现有限温度的均匀d-波超导响应很弱，而电荷密度波的关联较强。在超导特征温度以上，他们还发现了磁化率在 $T^*$ 以下随降温被抑制的现象，且 $T^*$ 随着掺杂的增加而下降，这些都与铜氧化物中的赝能隙特征类似（图1）。格林函数的计算表明，在赝能隙温区，费米面上的谱密度在 $t^{\prime}/t>0$ 和 $t^{\prime}/t<0$ 两侧均出现了部分被抑制的现象，且费米面拓扑与对应的电子、空穴掺杂铜氧化物的ARPES实验观察吻合（图2）。此外，当掺杂接近半满时还存在反铁磁涨落区域，且 $t^{\prime}/t>0$ 一侧的反铁磁区宽于 $t^{\prime}/t<0$ 一侧，这也与铜氧化物的行为类似。

图1：宽度6的圆柱面上 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型的有限温度掺杂相图。(a)展示 $t^{\prime}/t=0.17>0$ ，对应电子掺杂情形，(b) 展示 $t^{\prime}/t=-0.17<0$ ，对应空穴掺杂情形。相图包括了超导（SC）、赝能隙（PG）、反铁磁（AFM）、电荷密度波（CDW）和高温相（HT）等。红色点划线表示估计的超导特征温度 $T_c^*$ ，绿色虚线表示磁化率峰值温度 $T^*$ 。插图展示了费米面上的谱密度分布。

图2： $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型赝能隙区费米面上谱密度的计算结果以及与铜氧化物ARPES实验观测的比较。(a) $t^{\prime}/t=0.17>0$ 的计算结果，为了能与实验直接比较，已根据粒子-空穴变换关系将整个图案平移了(π, π)。(b)电子掺杂铜氧化物Nd2−xCexCuO4的实验测量结果[6]。(c) $t^{\prime}/t=-0.17<0$ 的计算结果。(d)空穴掺杂铜氧化物Ca2−xNaxCuO2Cl2的实验测量结果[7]。

这项工作表明 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型的确能够抓住铜氧化物高温超导体的一些关键特征，比如穹顶状高温超导区、费米面上谱密度被抑制的赝能隙现象等。同时，宽度6圆柱面上的计算显示 $t^{\prime}/t>0$ （对应电子掺杂）的超导关联显著强于 $t^{\prime}/t<0$ （对应空穴掺杂），但在铜氧化物中则与之相反，空穴掺杂的超导范围更大、温度更高。这些结果显示要更加精确地描述铜氧化物高温超导体，建议要对 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型进行适当扩展，考虑实际高温超导材料中未包含在 $t\mathrm{-}t^{\prime}\mathrm{-}J$ 模型的其他相互作用，并适当考虑电声作用的影响等。

理论物理所苏刚研究员、李伟研究员，复旦大学戚扬研究员为工作的共同通讯作者，博士生屈代维为该论文的第一作者。该工作的合作者还包括理论物理所的博士生李乔依和大湾区大学龚寿书教授。本工作得到了国家自然科学基金委优青项目、重点项目，院稳定支持基础研究领域青年团队等项目支持。计算工作在理论物理所先进计算平台上完成。

正文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.256003

参考文献

[1]H.-C. Jiang and S. A. Kivelson, High temperature superconductivity in a lightly doped quantum spin liquid, Phys. Rev. Lett. 127, 097002 (2021).

[2]S. Gong, W. Zhu, and D. N. Sheng, Robust d-wave superconductivity in the square-lattice t-J model, Phys. Rev. Lett. 127, 097003 (2021).

[3]S. Jiang, D. J. Scalapino, and S. R. White, Ground-state phase diagram of the t-t’-J model, Proc. Natl. Acad. Sci. 118, e2109978118 (2021).

[4]X. Lu, F. Chen, W. Zhu, D. N. Sheng, and S.-S. Gong, Emergent Superconductivity and Competing Charge Orders in Hole-Doped Square-Lattice t-J Model, Phys. Rev. Lett. 132, 066002 (2024).

[5]理论物理所2023年重要科研进展四“二维量子格点模型有限温度多体计算方法取得进展”

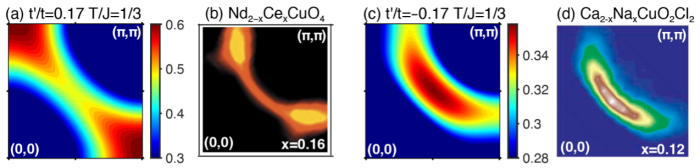
[6]H. Matsui, T. Takahashi, T. Sato, K. Terashima, H. Ding, T. Uefuji, and K. Yamada, Evolution of the pseudogap across the magnet-superconductor phase boundary of Nd2−xCexCuO4, Phys. Rev. B 75, 224514 (2007).

[7] K. M. Shen, F. Ronning, D. H. Lu, F. Baumberger, N. J. C. Ingle, W. S. Lee, W. Meevasana, Y. Kohsaka, M. Azuma, M. Takano, H. Takagi, and Z.-X. Shen, Nodal quasiparticles and antinodal charge ordering in Ca2−xNaxCuO2Cl2, Science 307, 901 (2005).

上一篇: 基于“慢速激光”的高能离子加速方案下一篇: 声波旋舞，晶格呢喃：手性声子的软化与手性电荷密度波

附件下载:

科学研究

铜基高温超导t-t'-J模型的有限温度掺杂相图、超导电性及赝能隙