组合优化问题起源于18世纪的哥尼斯堡七桥问题，现今在科学界和工业界的多个领域都具有极其重要的地位，其研究和应用广泛影响着科学、工程、经济和社会的各个方面。在这些具体应用领域中，实际问题往往可以抽象成具体的组合优化问题进行求解。著名的组合优化问题例子包括旅行商问题，它研究如何找到访问所有城市的最短路径；最大割问题，它研究如何把一个图的顶点分割成两个组，使得组之间的连边数目最多，等。 这些问题往往需要在庞大的变量空间中寻找具有最低目标函数的变量赋值，就如同大海捞针一般困难。在数学上，很多组合优化问题属于NP难问题，这意味着严格求解的计算代价往往随着变量数目指数增加。在实际应用中大家往往关心如何快速地找到目标函数比较低的变量赋值，这就是所谓的“启发式”算法。

图1：组合优化和自旋玻璃问题中复杂的能量景观示意图。如何跨过由能量壁垒所隔绝的能量极小点找到全局能量最低的解，是一个困难的问题。图片来源：Joshua Sortino,Unsplash

    组合优化问题在统计物理中被称为自旋玻璃的基态能量问题。在统计物理中，变量赋值映射为自旋构型，目标函数映射为自旋玻璃系统的能量函数，求解目标函数最小的变量赋值即为求解系统零温下的玻尔兹曼分布。从统计物理的视角看，求解自旋玻璃基态问题的困难之处在于系统的能量景观非常复杂，存在各种由能量壁垒所隔绝的能量极小值。如图1所示，在复杂的能量景观中寻找最低能量的基态构型很容易陷入局域最小而无法一览全局。为了应对这个挑战，统计物理领域发展出了平均场、消息传递等方法，为组合优化问题算法提供了非常重要的启发，创建了模拟退火等已经在科学和工业界广泛使用的经典启发式算法。模拟退火算法利用马尔可夫链蒙特卡洛方法在给定温度下的玻尔兹曼分布中抽样，同时逐渐降低系统温度，期望蒙特卡洛抽样可以借助这个退火的过程避免陷入局域最优，寻找到零温下的基态构型。模拟退火算法具有通用性，可以适用于各种不同的组合优化问题，因此不仅在统计物理领域，而且在科学与工程中的不同领域都有广泛的实际应用。然而，模拟退火算法依赖于马尔可夫链蒙特卡洛方法，通过基于当前构型来决定新构型是否被接受，进而逐步更新构型。因此，该算法本质上具有时间上的串行性，更适合在以CPU为代表的串行计算设备上运行。

    近年来，随着GPU和FPGA的快速发展，基于批量矩阵运算的高性能并行计算设备在算力上已经展现出了相对于CPU的显著优势。具体而言，单个CPU核心的处理速度可以达到4G FlOPs（floating point per second），但单个CPU往往只包含最多几十个核心。相比之下，GPU可以包含上万个核心，每个核心的计算速度也可以达到G FLOPs，从而在批量矩阵运算等任务中具有快得多的运算速度。因此，我们迫切需要发展新的统计物理的计算方法，高效利用GPU等并行计算设备所提供的先进计算能力，更高效地求解具有挑战性的自旋玻璃和组合优化问题。

    近期，中国科学院理论物理研究所的张潘研究员及其博士生沈子松，新加坡科技设计大学助理教授潘峰（此前为中国科学院理论物理研究所博士生），国科大杭州高等研究院博士生门一丁、硕士生徐闻彪与合作者们在《Nature Computational Science》发表了一篇名为“Free-energy machine for combinatorial optimization”的研究论文，提出了一种高效且通用的组合优化问题求解方法，称作Free Energy Machine（简称FEM）。FEM将统计物理学中的自由能最小化方法原理、平均场理论、模拟退火思想与机器学习中的自动微分与梯度优化技术相结合，用于高效求解一般的组合优化问题。在FEM中，给定温度下的玻尔兹曼分布由平均场近似来描述。这个近似将n个变量的联合分布概率分解为n个边际分布概率的乘积，平均场变分自由能可以写成边际分布的函数。在给定温度下，FEM将变分自由能作为损失函数，通过自动微分和梯度优化学习到一组边际分布概率，从而使得变分分布在平均场的框架下尽可能接近玻尔兹曼分布。然后通过一步一步地降低温度，持续不断地更新边际分布概率，最终有效表达由基态构型们所组成的零温玻尔兹曼分布，从而找到近似的基态能量以及与之对应的构型。在整体思路上，FEM与模拟退火算法非常接近，都是通用的算法，可以应用于包括q个变量取值状态以及具有多体相互作用的不同的组合优化问题，通过降温来逼近零温的玻尔兹曼分布。不同之处在于模拟退火算法利用马尔科夫链蒙特卡洛串行得到的构型来近似表述不同温度下的玻尔兹曼分布，而FEM通过平均场变分分布来表述。FEM变分分布的参数可以并行更新，因此可以高效地利用GPU和FPGA等并行计算设备进行极大地加速，可以在短时间内高效求解大规模组合优化问题。图2展示了FEM的原理。

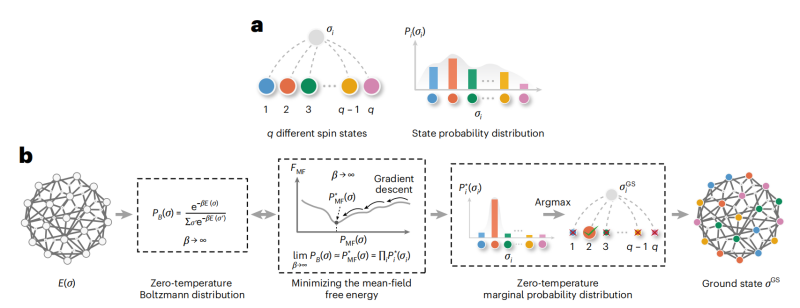
图2：(a)每个变量可以有q个不同的状态取值（左），状态取值的概率由边际概率分布确定（右）。(b) 组合优化问题的最优构型可以通过变分平均场自由能最小化结合退火的方式进行推断得到。

    为了评估FEM的性能，论文中在各种不同类型的组合优化问题上展开了基准测试，包括最大割问题（Max Cut）、平衡最小割问题（balanced Min Cut）以及最大满足问题（Max K-SAT）等。

    最大割问题是个典型的2态（变量取两种值）和2体相互作用的组合优化问题（也称为QUBO问题）。论文中在最大割问题的标准测试集G-Set上进行了测试，在54个基准测试数据中，FEM在其中的33个数据上超越了在这个问题的当前最优算法——模拟分岔算法（Simulated Bifurcation Machine），在其余的数据上也具有相当的性能。

    平衡最小割问题是个q态和受到平衡约束的两体相互作用问题。在这个问题上，论文中FEM与该领域最知名的两大专用求解器METIS和KAHIP（后者是第10届DIMACS算法挑战赛的冠军）进行了性能对比。对比测试涵盖了规模高达百万顶点的各种测试集。结果显示，FEM在求解质量上相较于METIS和KAHIP这些专用求解器有显著提升，解的质量提升最高可达26%。

    论文还测试了作为K体相互作用组合优化问题的代表——最大满足问题（Max K-SAT）。测试所用的数据集涵盖了2016年MAXSAT挑战赛的全部数据，在此数据集上与挑战赛中获奖的各类专用算法进行了性能对比。在454个赛题中，FEM均成功获得了已知的最优解。在求解速度方面，FEM表现出了显著的优势，相较于2016年MAXSAT挑战赛中的冠军算法，其速度提升了一个数量级。

    这些数值实验结果充分证明了FEM在不同类型的组合优化问题上不仅具有普适性，还展现出卓越的性能和求解效率。这进一步凸显了统计物理与机器学习相结合所蕴含的巨大潜力，使其有望在众多具有挑战的重要问题求解中得到广泛运用。

    此工作得到了国家自然科学基金理论物理专款前沿引领项目和华为合作项目的支持。

正文链接：

https://www.nature.com/articles/s43588-025-00782-0