弯曲的小宇宙:带空间曲率的拓展δN形式
在宇宙学中,原初扰动如何从量子涨落演化为今日宏观宇宙结构,是连接理论与观测的核心问题。特别是在暴胀理论框架中,曲率扰动ζ起源于暴胀场的量子涨落,它被拉出哈勃视界尺度后趋于常数,之后在热宇宙阶段重入视界并决定宇宙中的光子温度和物质密度分布。某些曲率扰动较大的区域甚至会因自身引力而坍缩至奇点,形成密度高到连光也无法逃逸的时空结构——这就是所谓的原初黑洞。这类天体是当前宇宙学和天体物理的研究热点之一,因为它们可能构成宇宙中暗物质的主要成分。
长期以来,"形式"作为处理曲率扰动非线性演化的有效工具,广泛应用于多种暴胀模型中。该方法基于"分离宇宙假设"——在超出哈勃视界的尺度上,梯度相关项迅速衰减,因此每个观测者所在的哈勃片区(即标题中所谓的"小宇宙")可认为是独立演化的、空间平坦的弗里德曼宇宙。形式告诉我们,这样一个小宇宙的曲率扰动正好等于局域膨胀指数相对于背景值的偏差,即。而是出视界时刻暴胀场初值的函数,因此在所有的小宇宙上呈现随机分布。这种方法由Sasaki等人提出,由于它物理清晰、计算简便,已成为早期宇宙学的理论支柱之一[1-3]。
然而,近年来的研究表明,在某些暴胀模型中(如暴胀进入"超慢滚"阶段时),传统的形式可能失效。原因在于,在这些非吸引子阶段,扰动在出视界之后仍会持续演化,空间梯度项在长时间内无法忽略,导致"分离宇宙假设"失效,形式也无法立即适用。如果要等待梯度项完全衰减再使用形式,则需要数值求解超视界尺度的暴胀场的非线性演化,形式的便捷性完全丧失了[4]。
为突破这一限制,中国科学院理论物理研究所的皮石研究员与京都大学Artigas Danilo博士、Takahiro Tanaka教授团队合作,提出了"拓展的形式"。该方法突破小宇宙的空间平坦性,首次在框架中引入每个小宇宙的空间曲率项K作为扰动演化的初始条件之一。通过巧妙选取初始等时超曲面的规范,可以将暴胀场扰动的梯度信息吸收到空间曲率的初始条件中,进而保留其对扰动超视界演化的影响。通过这一技巧,新的形式可以直接从扰动出视界的时刻起,持续精确地描述曲率扰动的演化过程,而无需等待梯度项的缓慢衰减。
研究以Starobinsky线性势模型举例。详尽的解析计算和数值结果对比表明,新方法在精度和效率上显著优于传统方法(参见图1)。此外,该方法还可用于计算扰动的非高斯性。结果显示在超慢滚阶段,非线性参数,符合皮石研究员与Sasaki于2023年提出的"对数对偶"的结果[5]。这说明该方法可直接用于计算曲率扰动的概率分布和原初黑洞的形成率,为相关研究提供了更可靠的理论工具。
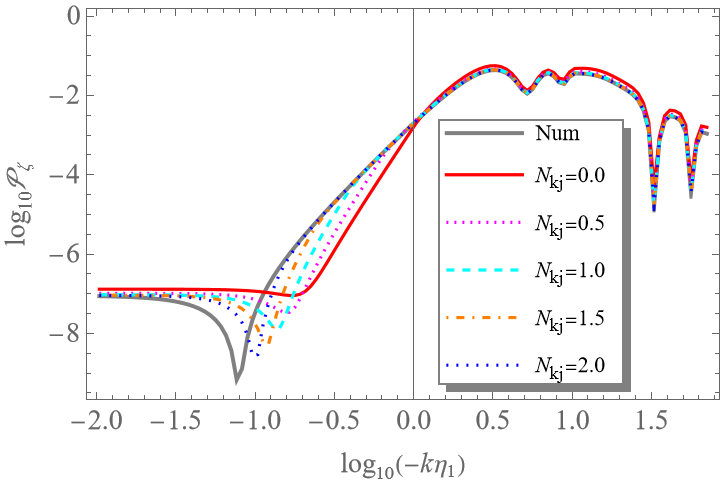
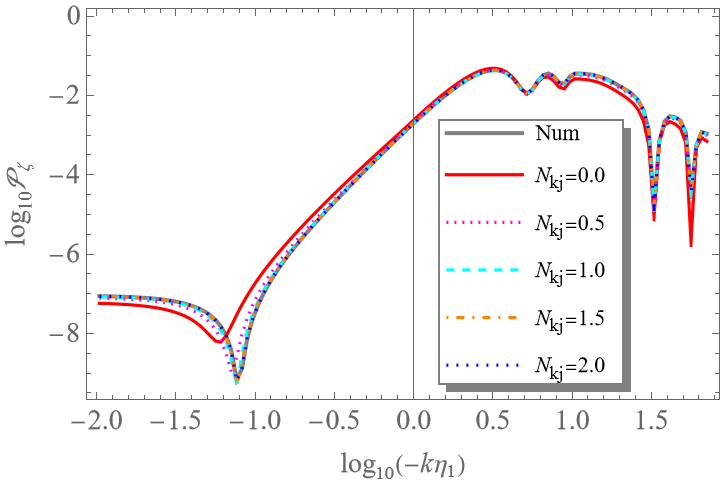
图1:方法(上)和拓展方法(下)计算Starobinsky模型中的曲率扰动ζ功率谱。可以看出,普通方法需要在扰动出视界后等待若干个哈勃时间才能适用,而拓展方法则可以立即使用,且与数值计算结果高度一致。细微的差别是由空间曲率K的高阶项引起的,可以忽略。
皮石研究员表示:"我们希望这项工作能为复杂背景下扰动的非线性演化建立更通用的框架。形式虽然经典,但只适用于吸引子相。此次拓展形式的提出,标志着这一基础宇宙学工具的重要升级,不仅拓展了其理论适用范围,也为原初黑洞形成、诱导引力波产生等前沿唯象问题的研究开辟了新的路径。"
该研究成果以《拓展的形式:非空间平坦的分离宇宙方法》为题发表在最近一期的Physical Review Letters上,皮石研究员和日本京都大学Danilo Artigas博士、Takahiro Tanaka教授共同担任通讯作者。该研究受到国家重点研发计划、国家高层次人才特殊支持计划青年项目、国家自然科学基金委面上项目、北京大学高能物理研究中心李政道青年学者项目以及日本学术振兴会的支持。

原文链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.221001
参考文献:
1.M. Sasaki and E.D. Stewart, A General analytic formula for the spectral index of the density perturbations produced during inflation, Prog. Theor. Phys. 95, 71 (1996) [astro-ph/9507001].
2.M. Sasaki and T. Tanaka, Superhorizon scale dynamics of multiscalar inflation, Prog. Theor. Phys. 99, 763 (1998) [gr-qc/9801017].
3.D.H. Lyth, K.A. Malik and M. Sasaki, A General proof of the conservation of the curvature perturbation, JCAP 0505, 004 (2005) [astro-ph/0411220].
4.J. Jackson, H. Assadullahi, A. Gow, K. Koyama, V. Vennin, D. Wands, The separate-universe approach and sudden transitions during inflation, JCAP 05 (2024) 053. [astro-ph.CO/2311.03281].
5.S. Pi and M. Sasaki, Logarithmic Duality of the Curvature Perturbation, Phys.Rev.Lett. 131 (2023) 1, 011002. [astro-ph.CO/2211.13932].


