量子纠错（quantum error correction）是在有噪声硬件上实现可靠量子计算机的重要基石。基于拓扑码（如表面码和色码）的传统方法已取得了令人瞩目的实验进展，但由于编码率低，通常需要数百万个物理量子比特才能支撑实际应用。为突破这一瓶颈，学界转向对量子低密度奇偶校验（quantum low-density parity-check,QLDPC）码的研究，这类编码在理论上可显著降低量子纠错所需的资源开销。其中，IBM近期提出的双变量双循环量子纠错码（bivariate-bicycle,BB codes）尤为引人关注，它在近期可实现的量子硬件条件下，有望将资源需求减少一个数量级 [1]。

近日，中国科学院理论物理研究所的研究团队（副研究员宋昊、博士生陈珂旸、硕士生刘媛婷）与中国科学技术大学（副研究员刘科、博士生张一鸣）及北京大学（助理教授陈昱安、博士生梁子健）的合作者一起，在此类量子纠错码的理论研究上取得重要进展。研究人员创新性地融合代数、几何与拓扑方法，建立了研究BB码的拓扑理论框架。相关工作以“Anyon Theory and Topological Frustration of High-Efficiency Quantum Low-Density Parity-Check Codes”为题，发表在《物理评论快报》（Physical Review Letters）[2]。

该研究工作主要有以下亮点：

一、引入“分形子”物理视角，确立拓扑序框架

研究团队注意到BB码与分形子（一类无法自由移动的新奇准粒子激发 [3,4]）物理在研究方法上的共通性，通过借鉴分形子领域发展出的代数工具 [5]，并结合Gröbner基等方法，成功实现了对任意给定BB码拓扑性质的高效表征。研究揭示，这类量子纠错码普遍具有以任意子为特征激发的拓扑序，但其任意子激发在短程移动中呈现出类似分形子的特征，即移动过程必然伴随能量的改变（图1）。

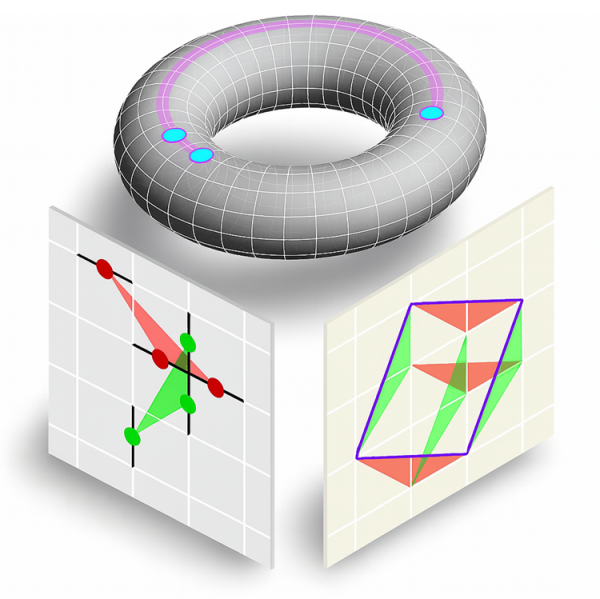
图1：环面上任意子的类分形子移动行为，以及通过牛顿多面体（红色与绿色三角形）的混合体积（紫色平行四边形）计算任意子种数的代数几何方法，其中牛顿多面体由相互作用量子比特的相对位置确定。

二、揭示“拓扑阻挫”现象，解析编码空间

研究还揭示了一种在BB码中普遍存在的“拓扑阻挫”现象。不同于传统拓扑码，BB码在环面上的基态简并度一般会小于任意子总数。研究指出，该现象与任意子的准分形移动行为密切相关，二者共同反映出平移对称性富化拓扑序（translation symmetry enriched topological order）这一深层次的拓扑物态结构。研究进一步利用Koszul复形的对称性质，阐明了在阻挫情形下，逻辑算符与任意子激发之间的精确对应关系。

三、引入代数几何方法，给出拓扑序变化规律

在方法论层面，该工作不仅利用Gröbner基等代数方法实现了对BB码的逐个高效表征，更创新地引入基于Bernstein-Khovanskii-Kushnirenko（BKK）定理的代数几何方法，揭示出在近环面码布局下BB码拓扑序的一般变化规律。通过BKK定理，任意子的种类可以通过计算由相互作用形式决定的牛顿多面体的混合体积（对于二维系统，即为牛顿多边形的混合面积，如图1所示）获得。

这些研究成果揭示了量子纠错、任意子激发、对称性与拓扑物态之间的内在联系，为发展新型高性能量子纠错码提供了重要理论支撑。利用这些数学物理原理，研究团队成员在同期发表于《PRX Quantum》的相关工作[6]中，将BB码推广到扭转边界条件情形，实现了纠错效率的进一步提升。

研究工作得到了国家自然科学基金委员会、中国科学院、安徽省、上海市和北京大学等的经费支持。