基于统计物理的量子纠错码严格解码方法
量子计算因其在密码学、量子化学模拟等领域的潜在优势备受关注,然而当前量子计算机在量子硬件层面容易受到噪声干扰产生错误,难以实现高精度计算。量子纠错是连接硬件与算法的核心桥梁,其目标是通过多个物理比特编码少量逻辑比特,通过测量辅助比特的方式用推断逻辑比特发生了什么错误并加以修正,从而抑制逻辑比特上错误的产生。
目前研究人员已经提出了各种各样的纠错码,如何从这些纠错码的辅助比特测量结果中推断逻辑错误的种类的方法被称为解码(decoding)。快速且精确的解码方法可以帮助量子硬件实现更低的逻辑错误率,但最优的解码问题在计算复杂度理论中属于#P难问题,如何构造高效的解码方法在量子计算领域仍然是一个重要挑战。 目前在例如谷歌量子计算团队所实现的纠错码实验中,普遍采用的方法最小权重完美匹配MWPM算法。通过此算法,谷歌量子计算团队在2023年的实验中实现了码距为25的重复码,展示了10−6量级的逻辑错误率;后续研究发现造成这一微小错误率的原因是宇宙中高能射线的影响 [1,2];在最近的实验中[3],谷歌量子计算团队采用码距29的重复码实验进一步将错误率降低到10−10,并推测错误的原因是未知的关联噪音。
注意到,为实现上述极低的错误率,解码算法至关重要,它必须尽可能精确,以避免引入额外的算法误差。然而现有解码算法MWPM虽然高效,却并不是理论最优的解码方法,因此有可能引入额外的逻辑错误。那么一个自然的问题是:存不存在理论上最优的解码方法,从根本上去除解码算法可能带来的逻辑错误呢?
近期,中国科学院理论物理研究所张潘研究员及其博士生曹涵彦、沈子松,国科大杭州高等研究院硕士生冯东阳,新加坡科技设计大学助理教授潘峰与北京量子信息科学研究院赵寿宽,严海生,苏唐,孙伟杰,徐晖凯,于海峰等合作者,共同解决了这一难题。他们的研究成果“Exact Decoding of Quantum Error-Correcting Codes”近期发表于《Physical Review Letters》,并被选为“编辑推荐”。该研究利用统计物理中伊辛模型的严格解,提出了一种名为“Planar”的解码算法,首次实现了在电路级噪声下重复码的严格最优解码,并精确求解了电路噪声下重复码的纠错阈值。张潘研究员与合作者将该方法应用于谷歌的实验数据以及量子院的超导量子芯片实验,获得了比经典MWPM算法更低的逻辑错误率,并指出谷歌实验中至少有四分之一的错误并非源自其声称的未知错误源,而是由于所采用的解码算法本身。
Planar方法的精髓是将纠错码的最优解码问题映射到统计物理伊辛模型的配分函数计算问题上,并利用平面图伊辛模型严格计算方法加以求解。下面以重复码线路级噪音模型进行介绍。图1 (a) 展示了一个码距为3的比特翻转重复码的线路。首先,通过辅助比特的测量定义了奇偶校验探测器,没有错误的时候这些探测器的结果都是平庸的;如果出现了非平庸的探测结果则意味着有些区域发生了错误,而这些探测信号可以被用来推断所发生的逻辑错误是什么。其中不同颜色的线路区域中发生的比特翻转噪音会改变图1(b)中相应颜色的奇偶校验探测器的测量结果。在这个例子中,所发生的逻辑错误只有两种:逻辑比特发生了比特翻转和没有翻转。从理论上,最优的解码方法需要计算这两种情况所发生的概率值。但是由于每种情况会对应到指数多个可能的错误构型(即所有区域上有没有发生错误的组合),概率值的计算需要把指数多个错误构型的发生概率进行求和。由此可见,这个计算与求和指数多个伊辛模型构型的权重来求配分函数是非常类似的。在这个例子中,我们会先将线路转换成为图1(b)中所示的纠错图,并将所有符合测量信号的错误构型的求和转换为这张图所对应的对偶图中自旋变量的求和。进一步,通过量子纠错的统计物理映射[4]我们将纠错图转换成图1(c)中所示的伊辛模型,此时逻辑错误的总概率就严格对应到此伊辛模型的配分函数求解了。 注意到这个伊辛模型中没有任何一条边会跨过另外一条边,因此我们称之为“平面图”伊辛模型。
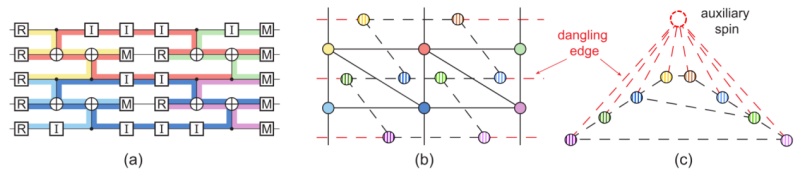
图 1:(a). 码距为3且重复观测轮数为2的重复码纠错线路。(b). 探测器噪音模型对应的纠错图(实线)及其对偶图(虚线)。(c). 增加辅助自旋后构成的平面伊辛模型示意图。
在理论物理领域,伊辛模型的严格求解,特别是Onsager 1944年提出的二维伊辛模型严格解,具有里程碑的意义:它证明了二维伊辛模型存在相变,为相变于临界现象提供了深刻的见解,并启发了后续统计物理严格理论的发展。在此工作中,张潘与合作者将有限大小平面图伊辛模型的一种严格求解方法,1952年所提出的Kac-Ward理论[5],用于纠错码所对应的平面图伊辛模型,从而提出了应用于线路噪音重复码的最优解码方法。此方法不仅解码精度高,计算速度也非常快,通过实验数据拟合得到的纠错时间复杂度为O(N0.82),其中N为对应伊辛模型变量的个数。
在论文中,作者用大量的数值实验验证了严格解码方法的优越性。首先,对于已知噪音模型(例如退极化噪声和超导SI1000噪音模型)的重复码,新方法首次得到了严格的纠错阈值,如图2 (a) 和 (b)所示;其次,在谷歌最新的量子存储实验的实测数据之上[3],论文作者对其重复码解码过程进行了重新解析并得到了比谷歌所使用方法更低的逻辑错误率,以及更小的“错误压低因子”图2 (c),也因此展示了谷歌实验中的误差至少有四分之一不是来源于其所宣称的未知错误源,而是谷歌所采用的解码算法;最后,北京量子信息科学研究院的团队在72量子比特的芯片上开展了不同码距的无重置操作重复码量子存储纠错实验。在相关实验数据上的解码结果展示了在非理想的噪音模型条件下Planar算法仍然有相较于MWPM的显著优势,如图2 (d)所示。
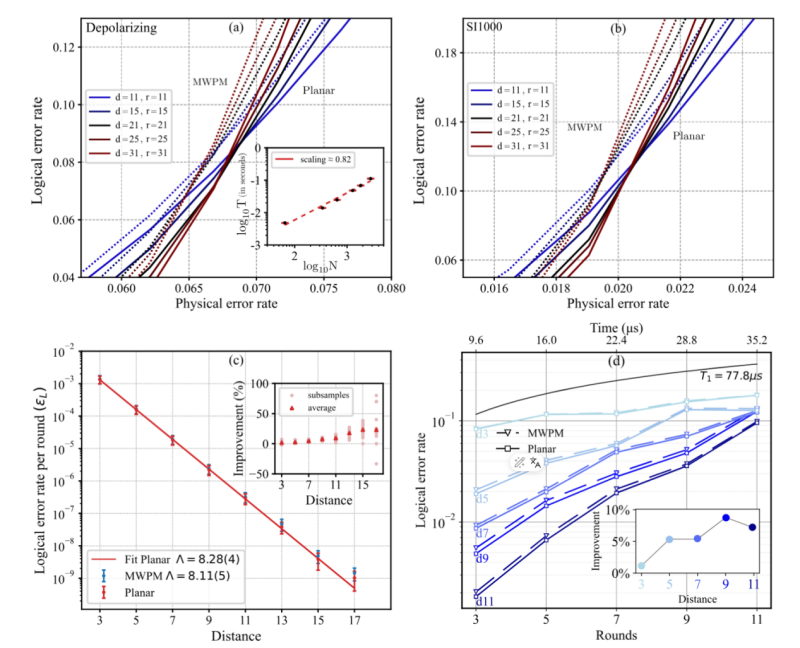
图 2:(a). 退极化噪音模型下重复码的的planar严格解码结果 (b). 超导 SI1000噪音模型下重复码的严格解码结果 (c).谷歌重复码量子存储实验数据的Planar解码结果。(c). 北京量子信息科学研究院72比特超导量子芯片上所实现的重复码量子存储实验的解码结果。
此外,该工作所提出的Planar解码方法具有普适性,可应用于所有最大似然解码问题可映射为平面图自旋玻璃模型的量子纠错码体系。例如,Planar方法可以适用于表面码(surface code)及其旋转变体(rotated surface code)在独立且无关联的码容量噪音下的解码。在文章的补充材料中作者详细给出了表面码到平面自旋玻璃模型的完整映射方法以及相应的数值结果。这些数值实验结果充分证明,相较于传统的MWPM,Planar解码器展现出显著优势。

正文链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.190603
论文代码:
https://github.com/CHY-i/planar.


