在量子力学中，交换统计是全同粒子的基本属性。根据交换统计的不同，构成我们宇宙的基本粒子可以分为两类：玻色子（如光子、希格斯粒子等）和费米子（如电子、夸克等）。在三维空间中，由于粒子的双重交换过程总是拓扑平庸的，因此基本粒子只能具有玻色或者费米统计。然而，在二维量子多体系统（如分数量子霍尔效应）中，却可以演生出背离玻色和费米统计的准粒子，即任意子。这一现象在过去的几十年里已经受到了广泛的研究。近年来，有关三维量子系统的研究也取得了长足的进展，其中，分形子（fracton）物态的理论发现暗示了即使在三维空间中也有可能涌现出奇异的交换统计行为。但是，由于分形子不具有常规的可移动性（这是分形子区别于传统粒子的全新特性），究竟交换统计的概念还能否适用于分形子这一类全新的准粒子成为了困扰研究人员的一个基本问题。

最近，理论物理所宋昊副研究员与合作者成功地解决了这个基本问题，给出了肯定的答案。该工作指出：虽然缺乏“一到一”的常规可移动性，但是分形子具有“一到多”的分裂移动性。通过分裂移动，单个分形子与一个分形子群体可以实现交换（图1）。这种“一对多”的交换方式（被称为“风车过程”）可以满足系统中所有的移动约束。该工作为粒子交换统计的研究开启了新篇章。它使我们能够定义分形子的自统计，例如，费米型分形子的含义。此外，该工作还揭示了在一些情况下分形子可以具有既非玻色型又非费米型的奇异统计行为。

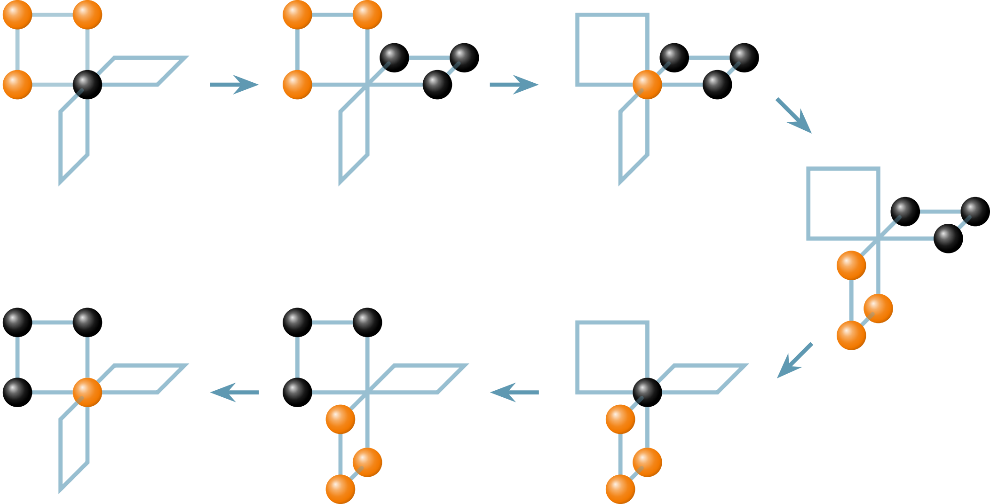
图1 “风车过程”实现了单个分形子（黑色）与一个分形子群体（橘色）的交换。

发现分形子自统计是对量子物态进行分类和表征的一个关键、不可避免的步骤。作为分形子自统计概念的重要应用，该工作证明了某些分形子物态，如著名的Haah编码与一个变种模型，如果不借助这一概念，是无法区分彼此的。分形子自统计的发现不仅影响凝聚态物理领域，还可能对量子信息存储理论和奇异量子场理的发展产生深远影响。

该项工作由中科院理论物理所宋昊副研究员、加州理工大学Nathanan Tantivasadakarn博士、普林斯顿高等研究院Wilbur Shirley博士及科罗拉多大学博尔德分校Michael Hermele教授合作完成。研究结果近日发表在Phys. Rev. Lett. 132, 016604 (2024)上，并被选为编辑推荐。

论文链接：https://doi.org/10.1103/PhysRevLett.132.016604