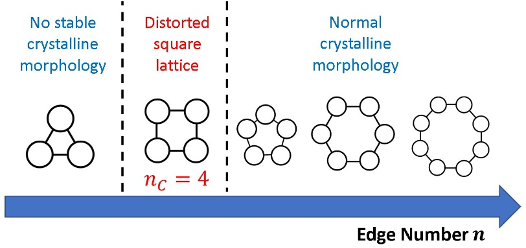
图 1、 不同边数正多边形晶体相稳定性的示意图。

中国科学院理论物理研究所（以下简称理论物理所）的软物质物理科研组通过对球棍正多边形（三角形、正方形、五边形、六边形和八边形）系统进行分子动力学模拟，揭示了一个临界边数  ，如图1所示[3]。边数少于4的多边形（三角形）系统在低于熔点的任意有限温度下稳定在类自旋冰的玻璃态。如图2a所示，这种结构的核心特征在于存在两种同构的元胞结构，二者可以任意混合。从原子团簇的视角来看，这个结构可以按照图2b的方式映射到一个定义在拓扑三角晶格上的、具有“4进2出”规则的自旋冰体系。

具有4条边的正方形正好处于临界情形，形成扭曲的四方晶格，如图2c所示。我们的分析表明，这种晶格一方面具有自相似的平移对称性，另一方面具有相当高浓度的拓扑缺陷，如图2d所示，该图中每个Voronoi元胞按照其边数进行染色。在较高温度下，这个扭曲的四方晶格直接熔化为液体，没有出现相应的硬正方形体系熔化相变中存在的六角中间相。

对于具有五条或更多边（六条、八条）的多边形，它们在有限温度下都呈现出常规的晶体形貌。通过比较不同多边形晶体的熔点，我们发现，边数更多的多边形在高压下总是具有更高的熔点；然而六边形由于相互作用和形状的完美匹配，在低压下表现出异于五边形和八边形的超稳定性。这些结果表明热稳定性存在两种相互竞争的物理机制：高压下由熵主导，而低压下由焓主导。

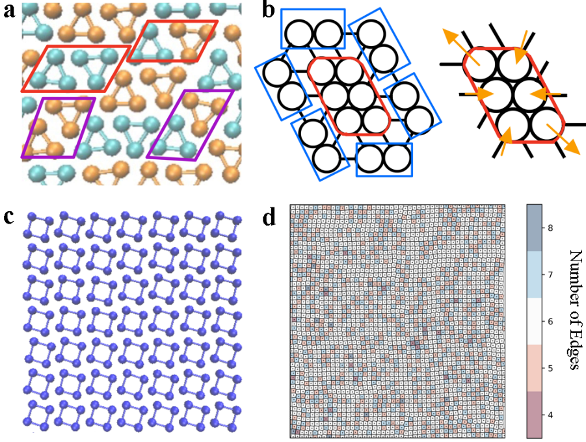
图 2、 球棍三角形形成的类自旋冰相和球棍正方形形成的扭曲四方晶格。图(a)中不同颜色的框用以强调两种同构的元胞结构。从中心的原子团簇来看，每个团簇具有6个近邻团簇，因此可以以图(b)的方式映射到基于拓扑三角晶格的“4进2出”的自旋冰体系。图 (c) 展示的扭曲四方晶格具有明确的四重对称性，但从图(d)可以看出其拓扑缺陷浓度相当高。

六角相是否存在是二维相变研究的核心关注点之一。前人基于对硬多边形体系的模拟，总结出了一条唯象规律[4]：当固相和液相的局域对称性匹配或取向熵足够弱时，六角相就会出现。我们的研究发现：这条规律对于具有常规晶体相的多边形仍然适用，但在考虑具有内禀无序性的体系（球棍三角形和四边形）时则失效——这类体系在熔化过程中不出现六角相。

本文的所有结果都可以在熵焓竞争的框架下得到统一解释。由于相互作用球位于多边形顶点，形状和相互作用各自诱导的对称性在空间上相互冲突。这种冲突在边数较少的多边形中更为强烈，因此更难形成有序结构。在热力学层面，熵和焓的竞争同样存在，从而导致相稳定性由两种相互竞争的物理机制所决定。虽然这一理论框架来源于简化模型，但是它具有向更加复杂和普遍的二维体系推广的潜力。

最后，尽管球棍多边形体系相较于实际分子体系仍然是简化的，但它凸显了实际二维体系的两个重要因素：形状和相互作用。过去的研究表明[5]：不同尺度的物理体系在这两个方面具有共性时，即使单体之间的吸引力具有完全不同的物理特征，它们仍然能够呈现出相同的平衡态或非平衡组装结构。因此，我们的工作有望促进二维分子材料的系统设计和高效利用。例如，拓扑自旋冰态应当具有超出常规自旋冰模型的物理性质和应用场景；扭曲晶格可以用于调控材料的力学性能或能带结构等。

这项研究成果近日在 Nature Communications 期刊上发表，理论物理所硕士生朱睿健同学为论文第一作者，王延颋研究员为通讯作者。作者感谢与理论物理所孟凡龙教授、金瑜亮教授、香港科技大学韩一龙教授和中国科学院理化研究所研究生陶锟同学的有益讨论。这一工作得到了国家自然科学基金理论物理专款“彭桓武理论物理创新研究中心”和中国科学院大学本科生科创计划的支持，计算工作在理论物理所先进计算平台和天河2号超级计算机上完成。