曼妙的旋律固然使人心安神宁，但刺耳的噪声偶而亦令人感悟到自然之深邃。譬如，从回响在浩渺宇宙的电磁波的噪声中，人们可以捕到大爆炸的余烬——微波背景辐射；从流过量子霍尔导体的电流的噪声中，人们可以瞥见费米子携带着分数电荷分身散影；而非平衡统计物理的支柱之一——涨落耗散定理——则建立了复杂微观运动引发的噪声和宏观输运现象普遍而简洁的联系。

    随着人们对统计物理理论理解的深入和凝聚态物理、量子信息等领域的发展，量子纠缠已成为多体物理的核心概念之一。然而，由于纠缠熵、Rényi熵、子系统复杂性等纠缠度量具有信息论性质，与传统物理量如电荷、电流等截然不同，纠缠动力学的理论研究有相当大的挑战性，严格结果极为稀少。即便是对Rice-Mele模型这样简单的无相互作用多体系统，对一般的初始波函数，人们尚无法从数学上预言其纠缠熵的长时间演化图像。因此近二十年来，对纠缠演化的理解很大程度上依赖于Cardy、Calabrese等的一个结果，即对Rice-Mele等无相互作用多体模型，若初始态为高斯态且系统无限大，则纠缠熵在经历早期线性增长后达到饱和，呈现出一个平台。据此物理图像，纠缠熵进入平台期后不展示涨落。但是，该图像仅在上述极为苛刻的条件下被证明，在对许多模型的真实或数值实验中，人们都观察到了与此图像的显著偏离，尤其是非平衡涨落的普遍存在。这些观察是否预示着全新量子涨落效应的出现？对此课题的探索已然超出了现有的纠缠和统计物理理论。实际上，Deutsch等当代统计物理杰出学者已开始探讨纠缠的非平衡涨落与统计物理理论基础的联系，但都是基于数值实验。

    最近，中国科学院理论物理研究所田矗舜研究员和浙江大学林励庆副教授及其博士生娄存忠合作，对一大类自由和相互作用可积格点模型发展了一个非平衡纠缠涨落的严格数学理论。依此理论，他们“听”到了量子纠缠在时间演化过程中发出的奇特噪声（附图左）。相关成果近日刊载于《自然·通讯》。

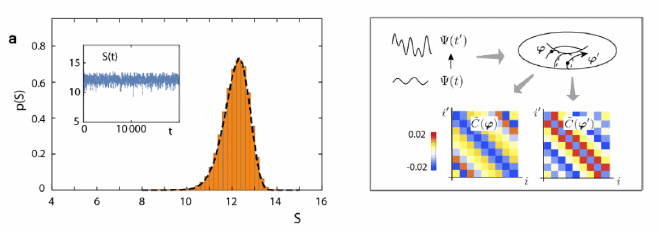
附图：纠缠在时间演化过程中涌现出普适介观涨落现象（出自论文）。

    研究团队在46页补充材料中阐述了该理论的构建。它由两个核心步骤组成。

    本文通讯作者为中国科学院理论物理研究所田矗舜，第一、第二作者分别为浙江大学林励庆和娄存忠。此工作得到了国家杰出青年科学基金、中国科学院理论物理前沿重点实验室和国家自然科学基金理论物理专款“彭桓武理论物理创新研究中心”及面上项目的支持。