宏观物理量的计算不仅是统计物理中的核心问题，更是在机器学习、组合优化、量子多体与量子计算等广泛的领域中扮演着重要的角色。然而相互作用系统的微观构型数目往往随系统规模的增加而指数增长，宏观物理量的计算需要指数级别的计算复杂度，难以在可接受的计算开销下得到精确求解。为了解决这一问题，研究者们发展出了众多近似算法。在这些算法中，在统计物理与网络科学中有着奠基性地位的消息传递算法，和近年来在凝聚态物理等相关领域大放异彩的张量网络方法，都利用了变量间相互作用的结构信息，将多变量的构型概率分解为两变量概率因子的乘积。在图论的语言下，这对应于在存在相互作用的变量间建立连边所得到的图。但是，这两种方法各自有着明显的优势和劣势——消息传递算法无视了图上所有的圈结构，一律按树图上的规则进行迭代，因此其拥有线性相关于系统规模的低计算复杂度，但这也导致它在包含短圈的图上表现很差。与之相反的，张量网络方法考虑了图上的所有结构，从而可以精确计算包含短圈的各种复杂结构，但由此付出的代价是更高的计算开销，尤其是长圈的增加，会使得张量网络缩并的计算复杂度快速增长，大大限制了可处理系统的规模。

    针对这个难题，中国科学院理论物理研究所张潘课题组系统地发展了任意图的张量网络方法[1-4]，涵盖了从严格到近似、从固定线路到通用的张量网络网络的众多情形。进一步，张潘研究员及其硕士生王一佳、伦敦大学学院博士生张钰雯与新加坡国立大学博士后潘峰（此前为中国科学院理论物理研究所博士生）于近期提出了张量网络消息传递（TNMP）算法。TNMP方法结合了张量网络和消息传递算法的优点，同时解决了短圈和长圈结构所带来的问题。具体来说，TNMP算法在处理局部的多短圈子图时采用张量网络进行缩并，对于全局的多长圈环境则采用消息传递算法进行近似，既利用了张量网络在处理短圈结构时的优势，又保留了消息传递在处理长圈时的高效性，大幅提升了现有算法在宏观物理量计算上的精确度上限与规模上限。TNMP算法也可以被视为终极的圈展开平均场方法，利用张量网络方法严格地处理系统中圈的效应，圈的大小远远超过了例如Plefka展开，Kikuchi变分自由能方法等传统的圈展开平均场理论。

    TNMP方法具体展示如下：如图1所示，在计算变量i的单点磁化率（即边缘概率）时，TNMP将相互作用系统对应的张量网络划分成两个部分：虚线圈中彩色的部分所对应的中心点i的“邻域”，以及圈外灰色部分所对应的“环境”。其中，邻域中的点与中心点有着更强的关联，于是在边缘概率的计算中扮演着更重要的角色，同时，其作为网络的一个局部有着足够小的规模，可以在可接受的计算开销下被精确处理。因此，TNMP使用张量网络缩并来对邻域进行严格地计算。而对于邻域之外的环境，虽然其所包含的信息由于关联的衰减而在边缘概率的计算中产生更小的影响，但获得严格的环境却具有和全局宏观量计算几乎一致的计算复杂度，故而具有很大的近似空间。基于此，TNMP沿用了消息传递的架构对环境进行近似——用邻域边界上所有“空腔”张量（图中的紫色圆圈）的直积来近似环境所对应的指数规模的张量，并通过迭代过程来得到满足邻域边界条件的空腔张量。如图2所示，通过数值实验可以看到，TNMP在人工合成网络与现实世界网络上均展现出了显著优于MCMC算法、传统消息传递算法与近期提出的含短圈修正的消息传递算法[5-6]的计算能力。

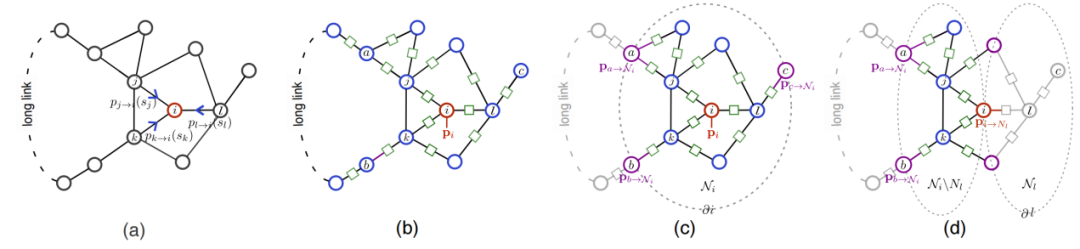
    图1：消息传递算法(a)、张量网络方法(b)、张量网络消息传递算法计算单变量边缘概率(c)与计算空腔张量(d)的图示。

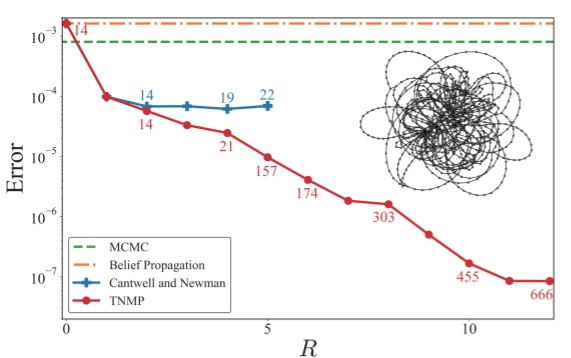
    图2：TNMP在人工合成网络[7]上的铁磁Ising模型（左图）与现实世界网络[8]上的自旋玻璃模型（右图）中均表现出了优越的计算精确度，并有能力在可接受的计算成本下达到机器精度。

    除了在多种图结构下的统计力学问题中展现出显著的优势之外，TNMP更是可以直接应用于贝叶斯推断问题、包括渗流问题与社区发现问题在内的网络科学问题、经典或量子的冗余码纠错问题与组合优化问题等广泛的领域与场景之中。同时，通过将张量网络上的代数延拓到更丰富的代数类型，TNMP可以在量子多体计算、复本对称性破缺下的近似计算等更大的舞台上发挥自己的潜力。

    论文于近期发表于Physical Review Letters并被选为编辑推荐。